Origins and evolution of the socioepistemological program in Mathematics Education

Ricardo Cantoral

Department of Mathematics Education

 Cinvestav, Mexico

-.Introduction. I present an emerging theory in the field of mathematics education from its origins and evolution in a  longterm  research program, the socioepistemological program in Mathematics Education. Socioepistemology, as a system of reason, focuses on the problem of the constitution of mathematical knowledge within the population; it is a theory in which constructs are elaborations with an empirical basis. Under the socioepistemological approach, the legitimacy of all forms of  knowledge is assumed, be this popular, technical or educated, as all of them together constitute human wisdom. Other contemporary approaches examine only one of the forms of knowledge.

Socioepistemology. A research program The word Socioepistemology itself means a relationship to knowledge, a metaphor that locates knowledge as socially constructed. However, since mathematical knowledge has been socialized in non-school settings, its introduction to didactic systems prods us to a number of modifications to its structure and functioning which also affects the relationships established between students and teacher. By introducing in order to know in a didactic form, lectures that facilitate communication of mathematical concepts and procedures and, consequently, knowledge is depersonalized and decontextualized. Such consensus is reached at the expense of a loss of essence and original meaning, reducing knowledge to isolated and sequenced issues, often called knowledge "content" or "thematic units" of a subject. The lectures that validate the introduction of mathematical knowledge to educational systems and legitimize a new system of reason, receive the generic name, in this theory, of Mathematical School discourse, and are seen as means to achieve participation in the educational field. The consensus thus is achieved through certain losses that are the prelude to forms of exclusion resulting from the hegemony itself that they entails.

The socioepistemological program has proposed the redesign of Mathematical School discourse as a way to address cultural, social problems that accompany teaching activities in mathematics. For example, interest addresses the phenomenon of massification of education systems, without considering, a priori, a negative feature of contemporary education. We also entered in the analysis of the impact that produces the translation of educational works of a culture or a language to another, more broadly to study of the processes of colony-metropolis  subordination. It investigates the teacher empowerment related to knowledge to confront the exclusion that produces the Mathematical School discourse and which is also derived from questions of gender, ethnicity, and physical, social or employment status.

Under this research program, mathematical concepts and processes that are operated in a didactic act cannot be mathematical objects in the classical sense, educated ways of knowing  accepted by the mathematical community or educational noosphere expressed in the official curriculum, either explicitly or tactically. They can be notions, preconceptions, ideas in its germinal stage, actions, activities and practices involved in other areas of human activity such as construction of artifacts, technological innovations, engineering design, the field of science, techniques, crafts, commercial activities and such. This is because mathematics from the socioepistemological view is considered an essential part of the culture; a "living" element is created "outside" the classroom, but recreates "inside" it: mathematics was not invented to be taught and yet is is taught, it is used in different settings, let us say that it "lives" through the most basic actions of all human activities: housing construction, planting activities and weaving, development of protocols for the use of drugs or toxic, making recipes, designing wine tanks, calculating medical dosages, explicit mathematical conjectures, coordination of movements of a pilot landing on a difficult track, mathematization of biological phenomena, decision making for financial investments, interpretations of public opinion, simulation of continuous flows, barter-traditional markets, study of the consolidation of saturated fine soil, temperature regulatory mechanisms in the chemical industry ... are present also in formal education in science classrooms, physical, chemistry, biology, technology, workshop, reading and understanding ... and, of course, in math class. They are present in the daily practices of all human beings who classify, predict, narrate, compare, transform, estimate, adjust, distribute, represent, construct, interpret, justify, locate, design, play, explain, count or measure.

This paper is based on Cantoral (2013), the first contributions of the 90s  on three specific practices: prediction, stability and accumulation respectively developed by Cantoral, (1990), Farfán (1993) and Cordero (1994). Such practices have focused on designing educational interventions that change the understanding of classical theoretical notions in Mathematics Education, for example the notions of learning or contract are extended towards an unschooled educational field which may not correspond to institutional mathematical knowledge (extended class). Thus, learning is a polysemic notion that similarly is used by the behaviorist program (learning and behavior change), cognitive approaches (learning as change of representation) or sociocultural frames (learning as change of practice). The contract, meanwhile, concerns the explicit or implicit relationships between teacher and student when school knowledge is under construction; now they include considerations of social and cultural order that include historical, cultural and institutional construction and dissemination of meanings circumstances.

Thomas Kuhn influenced our approach to change our perspective on the notion of scientific change or more specifically on the idea of progress. At the start of the Socioepistemological program, we asked what it means to systematically improve mathematical learning processes, what are the conditions that favor them and what are the obstacles. Thus emerges the notion of discourse, first as mathematical discourse for school (Ímaz, 1987) and as Mathematician School discourse (Cantoral, 1987), in both cases as ways of articulating and discussing the notions of progress and learning that offered the possibility of educational intervention. Also influencing our view are Freire, Piaget, Varela, Ímaz and Artigue; and equally important, are Struik, Koyré, Lakatos, Toulmin and Bachelard, for their approach to history and philosophy of mathematics, or more broadly of epistemology of science, focusing on contextual, conceptual and procedural aspects rather than achievements and progress in the conceptual ground. These authors were crucial for the development of the socioepistemological program. They helped us explore how to understand mathematical learning without attributing a sense of absolute and universal truth (deductivist program) or a single valid rationality (positivist rationality).

Soon, in the socioepistemological program, we looked into the need for a rational reconstruction of mathematical knowledge that supports a contextualized rationality about who learns that accompanies the program of epistemological relativism about what, how, when and why they learn. In this way it was articulated the notion of change with a conception of learning related to the contexts and practices of reference. The notion of the practice of reference is drawn from research by Farfán (1993, 2012) on the processes of mathematization of Engineering in the eighteenth century. The practice of reference is structured and structures the mathematical and scientific work of a time ranging from the creation of the École Polytechnique in Napoleonic France, until the emergence of the role of the professional mathematician after World War II. With these findings and by a large number and variety of empirical evidence, the socioepistemological program strengthens its critical view in respect to the formalist tradition and constructivist approach of those years. Neither the formalist tradition, with its emphasis on the problem of knowledge from the point of view of the foundations or the formal structure, nor the constructivist focus, that does relativize the matter of logical demonstration and points to the heuristics of research, do not abandon their predilections for mathematical knowledge as center of theoretical metaphors, they seemed adequate.

. Origin of the theory and its dimensions Socioepistemology originated at the Mexican school of Mathematics Education in the late nineteen-eighties and extended to Latin America and other regions during the nineties in order to collectively address a major problem: to explore ways of mathematical thinking outside and inside the school, which could be spread socially and characterized by its effective use among the population. We knew the way of teaching was structured by the institution that conducts education (teaching action: classroom, family, community, school or daily life) and that this, in turn, was structuring the socialization of knowledge and therefore thought processes involved (Cantoral, Farfán, 2003, 2004); and that it would become a slogan which proclaims: no more a didactic without students, but less still a teaching without sociocultural scenarios. The new challenge was to shift the gaze from concept to practice. While it began with the study of educational phenomena systemically, taking the three basic poles of the educational triangle: the content of teaching, the learner and the teacher, regulated by a controlled learning environment, soon we realized the need for successive reconstructions at the theoretical level. A learning situation would have to incorporate sociocultural dimensions intended to mean that which produced the mathematical knowledge, but especially following some live mode by its use in the environments of the learners. We expanded the ideas of classroom, knowledge and society to accept, on the basis of empirical evidence accumulated, that such reformulation required the incorporation of a fourth dimension: the sociocultural dimension. With its insertion, the other dimensions were transformed, and systemic study of the constitution of mathematical knowledge was opened from a socioepistemological perspective, that is, emphasizing the processes of social construction of knowledge and institutional distribution. The program is finally formed by four dimensions: epistemological, didactic, cognitive and socio-cultural. Examples of the extended model are found in Reyes-Gasperini (2013), who incorporated the empowerment to Socioepistemology; Carrillo (2006), who incorporated affective factors in the social construction of mathematical knowledge, and Covián (2005), who analyzed the normative character of social practices taking a further step towards a characterization of learning that links the individual to his community.

Actually we postulate that to address the complexity of the nature of knowledge and its functioning cognitive, didactic, epistemological and social levels (Cantoral, 2013), one should problematize knowledge, situating it in the realm of the apprentice’s life, which requires of the shared redesign, orienting and structuring of the Mathematical School discourse with awareness of the high value given to social practices. Mathematics in addition, has developed under a stigma that links it to abstract objects, ahead of the social and external, to the individual. Our program reverses this idea, with mathematics as part of culture, developing by social mechanisms in the production of meaning. Languages, laws, morality, and religion are social emergences that would not be able to be created by individual subjects, but by collectives normatized in the course of their evolution. Then, the key question arises as to what produces the norm. The idea itself is a socially emerging, regulating collective development. This idea is what we employ to affirm that social practice is a social emergence with new functions of normative types, identifying, pragmatic and discursive--reflexive. The notion of social practice with demarcated functions is a theoretical emergence that appears to incorporate the social dimension to the "didactic-epistemological-cognitive" system of the Fundamental Teaching and, nowadays, is an integral notion that supports the same theory. Given the different meanings that we were using for social practice they failed to explain all the complexity of the study, it was then raised the notion of social practice itself as object of study. We wanted to locate rigorously the role of social practice in the passage from knowledge to know, to speak with a Socioepistemological sense and not an epistemology itself. In regard, it was useful to  associate "use" with "knowledge" to provide a space to "know," thus suggesting a notion of situational learning or learning context.

We postulate that mathematical knowledge, even that which we consider advanced, has a source and social function associated with a set of socially valued and normed practical activities. This does not mean that all knowledge obeys a necessity of an immediately practical nature to a concrete issue. Historians of science have sufficiently documented that some mathematical notions are not from successive abstractions or generalizations of the empirical. Rather, our hypothesis has a socioepistemological perspective since it establishes establishes a relationship between the nature of knowledge that humans produce and the activities through which and because of which such knowledge is produced. Mathematics under this approach is the basis of human culture as much as is play, art or language. Our research has shown, in recent years, the relevance and consolidation of this position according to the results obtained as well as the theoretical elaboration. It has followed a systemic approximation to the research that articulates the four dimensions of knowing (social construction of knowledge): its epistemological nature (how we know), its sociocultural tessitura (emphasis on the value of use), cognitive planes (adaptive functions) and modes of transmission via education (cultural heritage).

Knowing, as social construction of knowledge, is constituted through deliberate processes for sharing knowledge. It is constructivist, highly sophisticated and social mechanisms that produce interactions, express or implied, between mind, knowledge and culture. For the analysis of knowledge, it must be problematized, specifically, knowledge about polyphony between advanced thought processes, epistemology of mathematics and specialized human practices. Thus mathematical knowledge [to know about something] cannot be reduced to a formal, declarative or relational definition, a mathematical knowledge [knowledge of something], but must deal with its historicization and dialectization as fundamental constitutive  mechanisms.

An example about problems linked to mathematical analysis.  

We exemplify with problems linked to mathematical analysis that proved useful for the development of Variational Thought and Language (PyLV), (Cantoral, Farfán, 1998). Based on the development of four tasks, seeking to recognize the zeros of the derivatives up to order three of a given graphically analytic function, our Postgraduate projects were carried to show that despite the rule that a student may have to the derivation as process and calculation of simple and complex derivatives, but is able to reproduce the geometric meaning of the derivative as slope of the tangent line at a point or know some theorems concerning derivatives of real functions of real variable, like that which states that "if f is differentiable at a,then it is continuous at a" even with all this, will struggle to articulate and interpret the successive derivatives. I anticipated theoretically in teaching calculus, a singular phenomenon linked to learning, with students and teachers would occur. We would say that speech, as a system of reason, structures educational actors through a didactic custom Mathematician School, producing little conceptual understanding for the transfer of meanings. Synthetically produced an absence of noesis (conceptual apprehension of the object) derived from a lack of praxis (process knowledge and awareness). Noësis represents the experience as whole, through acts of understanding focused on the object of experience, such as perception, imagination, consciousness or memory. In regard, the statement socioepistemological short version would say no noesis without praxis.

Without the development of PyLV (praxis), it is impossible for a student to successfully address a set of tasks as those discussed below. One has difficulty in assigning meanings associated the type of relationships f and f 'and f and f '' (noesis), as the Mathematician School speech induces a greater emphasis on consecutive derived or relationships of the type f (n)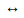 f (n+1),but does not analyze the type f (n) f (n+2) and even less f (n) f (n+3).The reason for this is linked to the way it is introduced into classroom the subject of the derivative of a real function. School presentation uses the incremental ratio limit, and be called derivative of f at a. The second derivative of the function f is defined as the derivative of the derivative function, as the third derivative of the function second derivative, and so on.

The concept to define is the first derivative of a function, being nested derived. This explains the chain between a derivative and its consecutive f (n)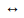 f (n+1), f(n+1)= . Hence, the hypothesis that the derivative may only be used in various scenarios when the successive derivatives are articulated to establish relationships up and down: f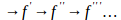 and. After the study reported in Cantoral (1990, 2013) it was problematized to knowledge and a route didactic solution was poured: The mathematical notion of derivative, which accompanies the practice of predicting, will be stabilized among students only when the derivative is used as a convenient articulation of the successive derivatives.

We maintained from those years that the main reason why it was not possible to articulate the successive derivatives in the classroom was due to the absence of scenarios sociocultural intermediation treated with processes of change and variation, since the limiting physiological order poses to humans a functional disability. We are not willing to perceive variations physiologically big order, particularly such limitation is given from the third order. It is impossible understand four people speaking simultaneously; we cannot "remember" bodily movements with varying acceleration; in the field of speech, we use to describe three states adverbs of time, before-now-after. We conclude that at the inability to perceive variations will, must articulate to variations lower order and assume constant to higher order. Thus, verbal interaction, we often reduce the comparative expressions two variations with three states. The set of states and the set of variations relate each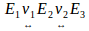 other. If states are not consecutive, an articulation of variations is 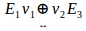required.Both forms of variation are illustrated as 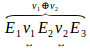follows:.

We exemplify this with a simple case. Consider that E1 represents the current height of a tree and E2 its height a year later, 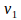then shows the increase in height, growth variation. If E3 is the height of the tree two years later, it shows the increment in height during the second year. So 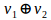in our model is the change of change, the change increases. In dynamic terms this is expressed as a function of time, locally linear. This formal but perceptible object, and calculable, it difficult to treat for higher order 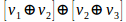variations. While unintelligible for students considering higher order to above: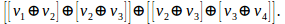

It is questionable whether such limitations on the interpretation of higher order variations have a localizable culture counterpart in daily practices. This was confirmed experimentally, since comparisons of "three states" characterize our usual discursive forms, culturally accepted for communication. These tripartite forms of neighboring states are constructed placing two extreme states invariably, the one and its opposite, to compare the evolution of a quantity or attribute. It is named E1 to smaller states and E3 and higher. It is then constructed an intermediate transition state, E2,with ambivalent characteristics participate characteristics extreme states. Examples of daily life are used to compare states. To compare temperatures, we use words: cold, warm and hot, corresponding respectively with E1, E2 and E3.To identify intermediate states and give the process variability dealing with states and intermediate positions, we use adverbs of quantity: very, very, very, little, much, more, less, so, so ... Something hot can be even "hotter" and it is said "very hot"; something "below" cold is very cold. Not so hot it is "just hot," "almost hot" or warm up. So in our speeches systematically we used the PyLV. The heights of people are distinguished between low, medium and high; positions relative closeness between near here and away; etc. Through the daily use of natural language, have been built adverbs of manner, time, location, amount or degree to deal with variational situations, a) Adverbs of manner: good, fair, poor; b) Adverbs of time: yesterday, today, tomorrow c) Adverbs of quantity or degree: none little much.

All these adverbs have a symmetrical and reversible structure that allows the speech a capital flexibility. The big-small or small large relationships translate immediately into relationships of growth, decrease or stability. The use of ordinary language precedes or accompanies the use of variations in Mathematics, as the student in a calculus course, has previously developed a discursive system to deal with the change and variation. However, in teaching this event sociocultural not part of the school content restrictions due to speech Mathematician School. If anything in his didactic discourse, the teacher who will vehicule variational strategies and schemes, as reported experimentally Resendiz (2004).

Let us use an analogy between the adverbial inflections and varying mathematical functions. We call each of these variations, both linguistic and mathematical, as variations of form I and II. Changes in the way I follow a pattern of sequential growth, step by step: Since a state is continued with the next state or to its predecessor. While variations of form II, follow a pattern of nonunitary jumps: given a state is passed to a nonconsecutive subsequent or previous state. The difficulty for analyzing variations of type II, lies in the absence of an a priori reference system, a site that serves as a source for measuring the variation; change as such does not exist without reference so it must be constructed in each case. The problem is who builds the source and reference system, over what? Decide what changes not enough to study the change. Perhaps because the absence of such origin in the reference system do not have words to talk about the third or fourth or fifth ... derivative. Why there no word to describe the change of acceleration? The position corresponds to the speed and acceleration, but no word accompanying the third derivative: What is concept? 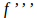Something similar happens with the graphic meaning of the derivatives. The function 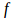represents the ordinate, the slope of the tangent line and 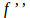the concavity of the curve, but what is the meaning for?

This difficulty is already peeking out from the management of the language itself, then use heat to two different 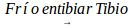 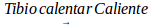 variations:,,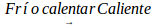

equivalently, we have the same situation for the inverse relationship:, . In classical physics, is understood not use a third variation, as Newton's second law states that the mass-acceleration system mass and acceleration are constant so it is not required of the third derivative. However, an answer must be sought within the framework of discourse School Mathematics. To address this task, there have been many experiments under the socioepistemological perspective. In all, interest has been explore how students compare, sequenced and articulate variations of higher order. For reasons of space I do not the numerous references should included in regard.

Final considerations. We can say without hesitation, that the PyLV has been the source of inspiration empirical socioepistemological program, the vast amount of research conducted by the working group finds it. However, have not been the only, most recently work on the periodic, the proportional, the analytic, playfulness, the professional, cultural, craft and others carried out in the Socioepistemology show a new path of research because the pair clearly incorporating social dimensions as empowerment or exclusion, focus their attention on proportionality as practical reference for a wide range of knowledge (Reyes-Gasperini, 2013b). Similarly find innovative to analyze processes deschooling of knowledge in practices such as circus malabar and planting and weaving in native communities (Espinoza, 2013; Yojcom, 2013, respectively) developments.

This chapter was intended to introduce the reader interested in the processes of social construction of knowledge to elements of an emerging theory: The Socioepistemology of Mathematics Education. This theoretical framework emerges, as we said, at a crossroads in an attempt to explain the relationships between mind, knowledge and culture in the field of mathematics relying on the notion of social practice. One does not film social practice, one abstracts; hence, the social practice as theoretical construct serves to explain the construction of knowledge based on practice, it deals with in consequence a construct from a significant pragmatic perspective which is therefore a construct from a pragmatic perspective of meaning. The existence of diverse practices, although similar to each other, in peoples and cultures, eras and regions, scenarios and circumstances, requires an explanation supported by the actions of subjects (individual, collective, historical) and in human activities mediated by culture.

A good example of what I mean what is “play.” It is certain that playing is a characteristic activity of the child, but it is also, in a wider sense, of all human beings. What is striking about this statement is not the fact itself that play is present in all cultures, but that the type of play held in different cultures have such similar structures including competitive games, strategy, strength or speed, cooperative participation ... and so many, equally games are practiced in India or Guatemala, both in the middle Ages as in recent years. Practiced in parks, public squares, plains, streets, houses ... for infants who, of course, know not "other children" of China or the Middle Ages who practiced similar games. How could they share their rules if they are so distant in time or space? While these games have different names from one region to another and practiced under small variations, always they have the common characteristic of being structured play. Rules structure play, characterizes the genre or game type and structure turn player practices. That is, play is structured and structuring ... The fundamental theoretical question posed by Socioepistemology, although not referred to as play, is the following: What causes the norm in the social construction of mathematical knowledge?

While in the field of social sciences the idea of of normed practice has been accepted by various theoretical approaches and is often used to explain various matters, this is not the case in the fields of exact sciences, and mathematics, as formal science, less yet. It is usual that, given such specialized field of human knowledge, it is assumed in the mathematics community that the creativity which characterizes ingenuity and learning is individually based, attributable to the capabilities of the inventor or the learner, and is therefore explicable on the basis of mental structures called talent or the exercise of free will of the one who performs the actions. It is usual for example, to hear that Gauss opened a field, Euler consolidated a branch, Newton extended a theory, in such ways that individuals are endowed with extraordinary talent who achieve these goals. The central question in this orbit of ideas is whether we could build an alternative explanation to the individual invention, an explanation focused on the processes of social construction of mathematical knowledge; hence to be this possibility, we will have with it a path to democratize mathematics learning among the population. That is, if we achieve an understanding of mathematics as akin to  play, as part of culture, we also will accept that they are guided by specific regulations. In this case, we must show empirically that different socioepistemological examples developed under the program can be explained based on the existence of nested practices, regulated by a social practice. More specifically we must show the existence of specific mechanisms of social practice, mechanisms that explain why we do what we do; normatize and structure the novice.

These are our new challenges, strengthen socioepistemological by designs for educational intervention with impact on educational systems and achieving greater theoretical rigor and therefore stabilize between the other theoretical field. A more detailed overview of this program is available in various publications Exclaim, the Latin American Mathematics Education Act and articles of Latin American Journal of Mathematics Education - Relime.

Referencias

Cantoral, R. (1987). Historia del Cálculo y su Enseñanza: El concepto de límite a través de los textos y de su historia. En F. Hitt, E. Bonilla y O. Figueras (Eds.), Mem. Prim. Reun. Centroam. Car. sobre Form. Prof. e Inv. Mat. Ed. (pp. 231–235). Mérida, México: Universidad Autónoma de Yucatán.

Cantoral, R. (1990). Categorías Relativas a la apropiación de una base de significaciones para conceptos y procesos matemáticos de la Teoría elemental de las Funciones Analíticas. Simbiosis y Predación entre las nociones de “el Prædiciere” y “lo Analítico”. Tesis Doctoral. DF, México: Cinvestav.

Cantoral, R. (2013). Teoría Socioepistemológica de la Matemática Educativa. Estudios sobre construcción social del conocimiento. Barcelona, España: Gedisa.

Cantoral, R., Farfán, R. (1998). Pensamiento y lenguaje variacional en la introducción al análisis. Epsilon 42(14, 3), 353–369.

Cantoral, R., Farfán, R. (2003). Mathematics Education: A Vision of its Evolution. Educational Studies in Mathematics 53(3), 255–270.

Cantoral, R., Farfán, R. (2004). La sensibilité à la contradiction: logarithmes de nombres négatifs et origine de la variable complexe. Recherches en Didactique des Mathématiques 24(2.3), 137–168.

Cantoral, R., Cordero, F., Farfán, R., Ímaz, C. (Eds.) (1990). Memorias del Simposio Internacional de Educación Matemática en el tema de Cálculo – Análisis. PNFAPM, Universidad Autónoma del Estado de Morelos, Universidad de Valencia, University of London. Toluca de Lerdo, Estado de México: UAEM.

Carrillo, C. (2006). ¿Saber sin sentir? Una introducción al dominio afectivo. Tesis de Maestría. DF, México: Cinvestav.

Covián, O. (2005). El papel del conocimiento matemático en la construcción de la vivienda tradicional: El caso de la Cultura Maya. Tesis de Maestría. DF, México: Cinvestav.

Cordero, F. (1994). Cognición de la integral y la construcción de sus significados: un estudio del Discurso Matemático Escolar. Tesis Doctoral. DF, México: Cinvestav.

Espinoza, L. (2013). El carácter político de la matemática y la transformación social. Memoria Predoctoral. México: Cinvestav.

Farfán, R. (1993). Construcción de la noción de convergencia en ámbitos fenomenológicos vinculados a la ingeniería. Estudio de caso. Tesis de Doctorado. DF, México: Cinvestav.

Farfán, R. (2012). Socioepistemología y Ciencia. El caso del estado estacionario y su matematización. Barcelona, España: Gedisa.

Ímaz, C. (1987). ¿Qué es la matemática educativa? En F. Hitt, E. Bonilla y O. Figueras (Eds.), Memorias de la Primera Reunión Centroamericana y del Caribe sobre Formación de Profesores e Investigación en Matemática Educativa (pp. 267–272). Mérida, México: Universidad Autónoma de Yucatán.

Reséndiz, E. (2004). La variación en las explicaciones de los profesores en situación escolar. Tesis de Doctorado. DF, México: Cinvestav.

Relime – Revista Latinoamericana de Investigación en Matemática Educativa. [Véase el sitio web] http://www.clame.org.mx/relime.htm

Reyes–Gasperini, D. (2013a). Empoderamiento docente desde una visión socioepistemológica: una alternativa de intervención para el cambio y la mejora educativa. Memoria Predoctoral. DF, México: Cinvestav

Reyes–Gasperini, D. (2013b). La transversalidad de la proporcionalidad. DF, México: Secretaría de Educación Pública.

Tall, D., Vinner, S. (1981). Concept image and concept definition in mathematics, with special reference to limits and continuity. Educational Studies in Mathematics 12(2), 151-169.

Yojcóm, D. (2013). La Epistemología de la Matemática Maya: Una construcción de Conocimientos y Saberes a través de Prácticas. Tesis de Doctorado. DF, México: Cinvestav.